Computer Software for Information Management

Enormous volumes of stored data are of use only if information can be retrieved quickly in an understandable form. Software for the purpose must reflect the structure of the data base and of the storage medium

by Michael Lesk

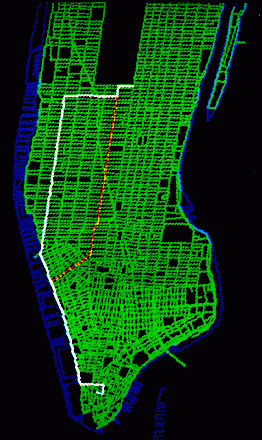
SHORTEST ROUTES TO THE PLAZA HOTEL from Wall Street were calculated by a computer program, which thereupon drew the map of the southern part of Manhattan Island shown on the opposite page. One route, shown in white, minimizes travel time and the other, shown in orange, minimizes distance. Because of the pattern of one-way streets in lower Manhattan, each route begins with a change of direction. The route that minimizes time passes along West Street to Tenth Avenue, which is followed uptown. Stored information about the average travel time on each street enables the program to specify the route that takes the minimum time. The route that minimizes distance begins on West Street, then passes uptown along Sixth Avenue. Software for storing and processing the information in the map was formulated by the author and his co-workers. The program for identifying the routes that minimize time and distance was written by one of those co-workers, Jane Elliott of AT&T Bell Laboratories.

As anyone with a cluttered office knows, having a large quantity of information on hand does not guarantee ready access to any particular piece of information. In the past two decades there has been a rapid increase in the capacity of electronic machines to store information and an equally rapid decrease in the cost of storage. In general the development of software for organizing and retrieving the electronically stored data has not kept pace. Those who are writing programs for information management are in the position of having to catch up with the capacities of the computing machinery.

What principles are guiding the effort? One principle is that the best form of organization depends on the content of the information and on how the information is to be used. For example, programs that maintain a list of names have been written for many purposes; they vary considerably according to what information is associated with each name and how the names are retrieved. A commercial system called Soundex is employed to identify airline passengers with reservations for a particular flight. Soundex stores the names phonetically, which reduces the number of transcription errors and allows a name to be found even if the exact spelling is not known. The Chemical Abstracts Service maintains programs for determining whether a particular substance has already been identified, a task that in a formal sense is similar to the one done by Soundex. The systems are not phonetic; furthermore, they record considerable information about chemical structure and nomenclature. Information specific to one domain of knowledge can improve the efficiency of a program in accomplishing one job, but the program then becomes less suitable for other purposes. Programs designed for a chemicals data base would be a poor choice for listing airline passengers.

Another consideration is the physical structure of the storage medium. Magnetic disks for storing data became common in the late 1970's. On a disk data are recorded in subunits called blocks, and access is most efficient if the logical divisions of the data approximate the boundaries of the blocks. Thus software aimed at managing large quantities of information is constrained on the one hand by the structure of the machinery and on the other hand by the content of the information. The effort to design software that more fully exploits the capacities of current machines is largely defined by the need to accommodate these two fundamental constraints.

A small group of related items in an electronic data storage system is generally referred to as a record. For example, in a file describing the stock on hand in a supermarket each record might include the type of product, the general category of goods of which it is a part, the number of the aisle where the product is to be found and the price. Each item in the record, such as the type of product, is referred to as a field. The record is retrieved from the electronic file by means of a key: a label that can consist of a field, a part of a field or a combination of several fields.

Some types of fields are employed as keys more frequently than others. It is probable that in the supermarket data base the aisle number would serve as a key but the price would not; hence the user could easily find all the products that are for sale in aisle 3 but could not easily find all the products that cost 49 cents. Other information, such as the name of the wholesaler that supplied the product, the shelf life of the product and the quantity of stock on hand might or might not be keyed. The software employed to manage the information should make it easy to search for the record that includes a particular value of the key.

It should be noted that the key need not be taken directly from the record. In formulating a directory-assistance system for AT&T Bell Laboratories I transformed nicknames in the storage record into their formal equivalents in the key. Thus "Chuck" in the record became "Charles" in the key. The transformation, however, was specific to the domain of telephone listings: in a geographic data base Billings, Mont., clearly would not be transformed into Williamings.

The varying relations among records, fields and keys serve to define the three main ways of organizing electronic records: the hierarchical, the network and the relational. The hierarchical system is so named because of the ordering of the fields in the record. In each group of records one field is designated the master field and the other fields are subordinate to it. Groups of records are arranged in a serial order resembling the rungs of a ladder and data can be retrieved only by traversing the levels according to a path defined by the succession of master fields.

Hierarchical data bases have been employed since the beginning of the modern period of machine computation in the 1940's and examples of their operation could be chosen from many fields. As a simplified example, consider the supermarket data base discussed above. The first level of organization in such a body of information could include a table giving the aisle numbers and the general category of goods available in each aisle. The category of goods serves as the master field. Only by retrieving the table of aisles and their contents and then selecting a category, such as produce, can the tables at the next level be reached. The second level of the hierarchy might include tables that list the specific products available in an aisle. The tables farther down might include the price of each product, the wholesale supplier and the product's shelf life. Only by traversing several levels of the hierarchy in sequence can information about a particular article, such as its price, be retrieved. Unless additional indexes are constructed within the file it is costly in terms of computer resources to ask questions that deviate from the hierarchical path, such as inquiring about the price directly.

The network model is somewhat more flexible than the hierarchical one because multiple connections can be established between files. Such connections enable the user to gain access to a particular file without traversing the entire hierarchy above that file. By this means the subsidiary connections modify the vertical structure of the data base in a significant way. For example, in the supermarket data base a connection could be established between the list of aisles and the table of prices, so that it would be possible to find the price of an article without first retrieving the intermediate table that identifies the products for sale in the aisle.

The relational model, which was developed by E. F. Codd of the International Business Machines Corporation in about 1970, is currently the subject of much interest because it promises greater flexibility than the other types of data bases provide. In both the hierarchical form of organization and the network form some questions are answered much more readily than others. Moreover, which questions are difficult to answer and which questions are easy to answer is determined when the data base is constructed. In many instances there is no sound basis for determining in advance what the most frequently asked questions will be.

In the relational data base flexibility is achieved by abolishing the hierarchy of fields. All fields can be utilized as keys to retrieve information. A record is not thought of as a set of discrete entities with one item being designated the master field; instead each record is conceived as a row in a two-dimensional table and each field becomes a column in the table. The entry
Aisle 2 Dairy Milk .69 quart
can be thought of as a relation between the aisle field, the general-category field, the product field and the price field. The relation could be augmented with the name of the wholesaler, the shelf life of the product, the quantity of stock on hand and other facts. Shorter relations consisting of two fields can be obtained from the full set of relations by choosing the appropriate fields; the process is referred to as projecting the relation. Thus the price of any product can be retrieved quickly, as could a table listing all the products in one aisle.

The classification of data bases into the hierarchical, network and relational forms is commonly cited in discussions of information management. The classification scheme is not as useful as it might appear, however, because the structure of any data base can be supplemented with secondary indexes that make it possible to answer efficiently queries that do not follow the underlying organization. Furthermore, certain problems are common to all three types of data base. Consider the task of selecting one record from a file made up of many related records. The file could consist of dictionary entries, the lines of a telephone directory or other records, but in all cases the problem is to retrieve one record quickly and efficiently. The case of picking out a single record depends critically on how the items are arranged in the main memory of the computer or on a secondary storage medium such as a magnetic disk. Several techniques for arranging data can facilitate subsequent retrieval; the techniques can be employed with any of the three types of data base.

For a small body of information it may not be necessary to maintain any particular arrangement. Lines can be stored on a disk in an arbitrary sequence; when an item must be retrieved, a simple pattern-matching program scans the lines sequentially for the appearance of particular combinations of symbols. In the Unix operating system, for example, a program named grep is often employed in this way. Suppose a list of telephone numbers, including those of two seltzer delivery companies, has been stored in a file named telnos. In the Unix system the command grep seltzer results in the printing of the names and numbers of the two companies that deliver seltzer. In the telnos file the word "seltzer" was entered before the name of the companies, but the key need not be at the beginning of the line for the grep program to operate. The command grep beverage < telnos results in the printing of the same two lines because the word "beverage" is part of the name of each company.

Maintaining a file of items that are not in a predetermined order has several advantages. There is the saving of time and effort that would be needed to sort the data when the file is set up. In addition considerable flexibility is maintained because it is not necessary to decide in advance which items in the file will serve as keys when the data are retrieved. If a system user decides to find all the numbers in the telnos file with the prefix 800, the command grep 800 < telnos works immediately, regardless of whether or not such a request was anticipated when the file was established. If the list is not ordered, new data can be added at the end of the file without rearranging the previously stored items. Furthermore, no space is required for storage beyond the space that is taken up by the individual entries. In more complex storage systems some memory capacity is taken up by information needed to organize the data.

The unordered method of storage has a critical drawback: retrieval is very slow. Each line in the file must be scanned separately and as a result searching a file of 10,000 lines takes 100 times as long as searching a file of 100 lines. The algorithm employed by the grep program corresponds to finding books in a library by starting at the shelves nearest the entrance and examining each book until the one wanted is found.

To speed tip the search process the file can be sorted into serial order, such as alphabetical order or numerical order. Putting the items in serial order makes it possible to retrieve an entry by the technique called binary search. The list is divided in half and the program determines which half includes the item sought. The process is then repeated until the item is found.

Suppose the file consists of the entries in a dictionary and the definition of "cat" is sought. A binary-search program would first identify the middle item in the dictionary, which turns out to be "legality." By comparing the first letter of "legality" with the first letter of "cat" the program determines that "cat" is in the first half of the file. The midpoint of the first half is "distort" and so "cat" is in the first fourth of the dictionary. After the next division, at "castigator," the second portion rather than the first must be searched. By continuing through the sequence of midpoints, the definition of "cat" is isolated.

Binary search is quicker than searching an unordered data set. Assume the file to be searched includes n items. On the average finding any one item by -searching through an unordered set requires n/2 operations. Binary search requires at most about log2n operations to find a particular item (where log2n is the logarithm of n to the base 2). The serial order has another advantage: When an entry has been located, it is a simple matter to find out about adjacent entries, such as the word after "cat" in the dictionary.

Adding a new entry to a file set up for binary search, however, is a costly process because the sorted order of the file must be maintained. Since a new item will on the average be inserted in the middle of the list, half of the items the file must be moved each time a new entry is added. The fact that entries can be found only from the key on which the file is sorted can also be a serious limitation. It is possible to duplicate the item and store multiple files sorted according to different keys, but that consumes much additional space.

Another technique for retrieval from a sorted file relies on subgroups of adjacent data entries called buckets. The first entry in each bucket is stored in a table that serves as an index to the divisions of the file. If n items are divided among sqrt n buckets, with each bucket holding sqrt n items, a linear scan of the bucket index followed by a scan of the appropriate bucket to isolate the needed entry takes only slightly more than sqrt n operations. Although sqrt n operations is not as good as log2n, particularly for a large file, it is not unwieldy for a small file. Furthermore, programs for bucket storage are simple to write.

So far the best we have been able to do in searching a file is log2n operations. It is possible to improve on that figure by means of the procedure known as hashing. To understand the advantages of hashing consider the possibility of assigning a number to each entry in a file. If the number could be computed quickly by means of a simple algorithm each time an item is needed, the item could be fetched directly from the file without searching.

For the entries of a dictionary such an indexed array could be created in principIe by a straightforward method. Each letter of the alphabet can be assigned a number, so that the spelling of a word designates a unique number that serves as the word's address in memory. The trouble with such a scheme is that the memory space required is immense, and it would remain almost entirely empty; most combinations of letters, after all, do not spell an English word. To look at the problem another way, the difficulty is that the first letters of English words are not distributed evenly. For example, words beginning with c, s or t are much commoner than words beginning with k or w. If 100 words were assigned to 100 numerical addresses on the basis of their first letter, they would pile up in certain slots instead of filling slots l through 100 in a smooth distribution.

The most convenient solution is to formulate an algorithm that assigns a "pseudorandom" number to each word. The spelling of the word fully determines the pseudoramdom number, but words spelled differently can generate the same number. The algorithm is based on a mathematical expression called a hash function. In one possible hash function each character in the alphabet is assigned a numerical value and the values for all the characters in a word are summed to yield the pseudo-random number that serves as the address. If an effective hash function is chosen, the entries are distributed fairly smoothly throughout the indexed array, which is referred to as a hash table.

It is generally necessary to leave at least one-fourth of the slots in the hash table empty. Leaving some slots empty reduces the frequency of cases in which the same pseudorandom number is assigned to more than one item. When such a duplication, which is known as a collision, takes place, an additional algorithm is invoked to pick a slot for the second item. The algorithm might call for the next slot in the hash table to be filled; as an alternative a second hash function could be computed. If the distribution of entries is known, the table can be kept more than three-fourths full, but it is not common for the distribution to be known.

It should be noted that when a body of information is organized in a hash table, the hash function is computed each time an entry is sought. The hash function is simple to compute, and when it has been computed the entry is retrieved without additional searching. Hashing is therefore a very fast method of retrieval. Revising the file is also efficient since the items are not stored in a serial order that must be preserved by moving many items each time an entry is made.

The technique of simple hashing has a drawback, however, that makes it unsatisfactory for many applications. Because of the problem of collisions, the approximate number of entries must be known in advance so that a hash table of the appropriate size can be constructed. If many new items arrive unexpectedly, it may be necessary to recompute all the hash functions. In practice it is often not possible to predict the size of a set of data, and so it is inconvenient to have to choose the size of the hash table in advance.

Unordered files, buckets, binary search and hashing are all techniques in use today, particularly in conjunction with small data bases where ease of programming is a more important consideration than ultimate efficiency. Two methods developed in recent years are more commonly employed with large data bases: extensible hashing and B-trees.

Extensible hashing was devised to avoid the need to specify the size of the hash table in advance. A hash code longer than necessary is computed and only the part of the code needed to accommodate the number of entries on hand is utilized; the rest of the code forms a reserve against an increase in the size of the file. The details of extensible hashing are beyond the scope of this article, but the outcome of the method is to preserve the speed of hashing at a small cost in additional storage.

In all the variants of hashing, file entries are stored in the arbitrary order determined by the hash function. Any sequential relations that might have existed among items in the the original data set are lost in the storage process. For example, if a dictionary is stored in a hash table, words beginning with e are scattered at random through the array. As a result, when a word has been retrieved, it is not possible to obtain a quick answer to questions about entries that were adjacent to it when the words were in alphabetical order.

A B-tree does make it possible to efficiently answer questions about items that were neighbors in the original sequence. The B-tree is a mechanism for implementing binary search in which the repeated divisions of the file are incorporated into the data structure instead of being calculated by the algorithm. The B-tree has the form of an inverted tree: there are many categories (leaves) at the bottom and only one category (the root) at the top. Each category, or node, is made up of a set of keys for data entries.

At the bottom level of the tree each node includes a group of entries arranged in order without omissions. At the next level up each node includes one key from each node of a subset of the nodes at the bottom. The process of reduction continues to the top of the tree, where there is a single node. The tree is traversed from top to bottom with the keys in each node serving as pointers to nodes one level down.

If a dictionary were stored as a B-tree, the first node might contain the words "chromophore," "epicycle," "impolite" and so on, which constitute a set of dividing points for the alphabet. "Chromophore," the first key, could point to a node at the second level that includes the words "alfalfa," "apocryphal," "available," "binocular," "bully" and "celery." It can readily be seen that the second list includes dividing points from the beginning of the alphabet to the word "chromophore". Each item in the second group points to a more finely resolved list At the bottom of the tree the nodes point to the dictionary entries themselves.

The B-tree has become popular for several reasons. As noted above, a B-tree makes it possible to answer questions about the adjacent items when one item has been retrieved. In addition B-tree storage is relatively fast: a search requires roughly log2n operations and adding or deleting entries also requires roughly log2n operations.

One of the main reasons B-trees have been so widely applied is related to the physical structure of magnetic-disk storage. It is often assumed for the purpose of approximation that each search in a file takes about the same amount of time. It is only in main memory, however, that each search takes an unvarying period, and data bases large enough to be of interest do not fit in main memory. Large data bases are stored on disk, where there are two types of search with quite different retrieval times. The random-access time is the average time needed to retrieve a record from an arbitrary position on the disk. The sequential-access time is the time needed to retrieve the record following the one most recently accessed. In a typical machine the random-access time might be 30 times greater than the sequential.access time. An efficient program therefore maximizes the number of sequential searches and minimizes the number of random ones by retrieving relatively large groups of data each time a search is done. If the data are stored in a B-tree, the size of the nodes at the base of the tree can be adjusted to match the size of a disk block. Hashing cannot readily exploit the disk structure.

In the preceding discussion the methods for storing and retrieving data have been considered separately. In the design of an actual system, however, it is often necessary to combine several techniques to achieve the best operational result, as is suggested by several examples drawn from work I have done with my colleagues. One experimental program we have devised gives weather forecasts for any town in the U.S. If the user asks for the weather in a particular town, the program finds the closest place to the town where the weather has been recorded and reports the most recent observations. It then goes on to locate the nearest weather forecasts and reports them.

Presenting such weather information entails the use of three data bases and software for each one. The system relies mainly on a National Weather Service communications circuit that delivers six megabytes of weather information per day, including observations and forecasts. The observations are made at airports, which are identified only by a three-letter code; as a result two data bases are needed in addition to the one that holds the weather information itself. The first supplementary data base, a table that gives the latitude and longitude of each airport, is drawn from records maintained by the Federal Aviation Administration. The second, a table that gives the latitude and longitude of each U.S. town, is drawn from Bureau of the Census records.

The town data are stored as a B-tree. The weather reports are stored in a bucketed file where the U.S. is divided into small squares of latitude and longitude. When a set of weather observations arrives, the airport code is converted into a location by means of the B-tree and the information is stored in the appropriate bucket. When a request for weather information is made, the bucket is searched for the closest airport. If the data were in one-dimensional rather than two-dimensional form, the entire job could be done with B-trees, but B-trees do not accommodate two-dimensional data well. The weather service is often used by my associates who are going on trips and want to know the weather at their destination.

Another service we provide is a means of selecting information from news stories filed by the Associated Press. The program is currently experimental and has about 100 participants. Each day about 200,000 words are stored in the computer system. There are two main modes of access to the information in the news stories. In one mode the user picks current stories from a "menu" display; the stories are selected according to a few words that serve as the title in a computer-terminal display. About 40 people read a total of 840 stories per day on the average by picking them from the menu.

In the second mode of access readers are able to retrieve stories by means of a profile consisting of particular words, phrases or syntactical operations. Someone who wants to read about Mount Everest can ask for all the Associated Press stories in which the word "Everest" appears. Queries based on phrases such as "space shuttle" or on features such as the inclusion of "telephone" and "regulation" in the same sentence can also be answered. About 50 people maintain such standing requests and some 550 stories per day are sent out because they match a particular profile.

The systems I have described so far are all designed to store and retrieve information in the form of numbers or words, but it is also possible to process large quantities of information derived from graphic images. Consider the problem of storing a street map in a computer file and then employing the file to answer questions that would ordinarily be answered by consulting the map. The information in a street map can be reduced to two main types of data: the location of nodes and the location of edges. A node is a point where two streets intersect; an edge is the segment of a street that connects two nodes. The positions of nodes and edges could be converted into digital form by devices called digitizing tablets or scanners, but fortunately the conversion has been done by the Census Bureau. Our system for processing maps is based on data obtained from the bureau.

How should the maps be stored? The data are copious, and what is even worse from the point of view of storage, they are two-dimensional. The storage system must be able to accommodate both these properties. Several storage methods could do so, and to select one we considered the queries that the system should be able to answer efficiently. Four types of query are significant: finding the location of a building when the street number, the street name and the Zip Code are known; finding out whether two streets intersect and, if they do, locating the intersections; finding all the points that can be reached directly from a given point, and finding all the streets within a certain radius of a given point.

Two techniques for storing data plotted in two dimensions are the connection matrix and the k-d tree. In the connection matrix the only information that is stored is the list of all pairs of nodes that are linked by an edge. Such a file does not include enough information to support the map system because it is essential for the system to include street names and the locations of the nodes. The street names must be entered so that the program can determine when the route passes from one street to another The locations of the nodes must be entered so that a left turn can be distinguished from a right turn and also so that a physical version of the map can be drawn.

The k-d tree is a variant of the B-tree that can accommodate data in more than one dimension. In the k-d tree the descent from one level to the next-lower level corresponds not only to a progressively finer selection of data but also to a change of dimension. At each step the data are divided along the largest dimension. Thus in storing a digitized map of Chile the first division would be along the north-south axis, whereas in a map of Tennessee the first division would be along the east-west axis.

The k-d tree is an efficient means of storing two-dimensional data because breaking up the information along its largest dimension reduces the number of decisions that must be made to retrieve an item. The main problem in storing maps, however, is not to reduce the number of decisions in each retrieval but to minimize the number of disk blocks that must be examined. Like the connection matrix, the k-d tree cannot store street names with the streets and therefore the names must be supplied from a separate file. To speed the disk-retrieval operations a "patched file" was constructed that comprises two subfiles, with each subfile holding a different kind of information. One file is the master list of edges, drawn from Census Bureau data and from a table of extra information for each street. The Census Bureau data give the location of each edge and its name; the additional table designates one-way streets and limited-access highways and gives information about speed limits and average travel speed.

In the master segments file, as in the original Census Bureau data, each street is divided into segments short enough so that a segment intersects other segments only at the ends and also short enough so that the segment can be approximated by a straight line. A segment corresponds to a single record in the data base. Such a form of organization implies that for most streets each block requires a separate record. The records are sorted in alphabetical order according to street name.

Each record includes a field that indicates whether the segment is an ordinary street, a limited-access highway, an access ramp or another map feature such as a railroad, a river or a boundary line. For streets the record also includes the house numbers on each side of the segment, information about travel speed, the locations of the endpoints and the Zip Code on each side of the segment. By means of a binary search through the master file it is a simple matter to retrieve the location of any street address and list the intersections of any two streets. Thus the master file alone can answer the first two types of query.

The second file is a group of segments organized according to a patched format in which the area covered by the map is divided into squares 10,000 feet on a side. To draw a map that includes all the segments in a particular area the program scans the list of patches sequentially and then scans the relevant patches in the same way. A segment that appears in only one patch is stored once, but a segment that appears in more than one patch is stored in all the patches where it has an endpoint. The patched file is entirely derived from the master list. When changes are made, they are entered into the master list only; the patched file is then regenerated automatically.

When techniques for organizing and storing the information from the maps had been selected, the problem of providing an interface between the user and the system had to be solved. Most of the available computer interfaces are inferior to a printed map. On many printed road maps the ratio of the width of the -smallest printed character to the width of the map is about one to 1,000. Even on a high-quality computer terminal the ratio of the width of the smallest letter to the width of the screen is generally only about one to 125. Furthermore, most computer devices can print only horizontally; a few can also print vertically but almost none can print at intermediate angles. Because of these limitations many street names must be omitted from the maps that are produced from the digitized information.

To determine which labels should be omitted the program utilizes information about how big the labels are and also about which streets are important. It is assumed that the longer a street is, the more important it is for routing purposes; the assumption works well in practice. Information about the relative importance of streets is also employed to excerpt the maps so that large areas can be represented without excessive detail and to plot routes that traverse only large thoroughfares. For rapid processing it is convenient to assume that each street follows a straight path between the intersections that survive the excerpting.

The system we have constructed can efficiently answer all four types of query given above. When the data base is combined with a program written by Jane Elliott of AT&T Bell Laboratories, it is possible to find the shortest route between two points on the map in terms of time or distance. Most of the map processing utilizes the patched-file structure, which is analogous to the bucketed file employed for one-dimensional data. The patched file is somewhat slower than the B-tree but it exploits the disk structure better than the B-tree does. The list of patches for a single map generally fits in one disk block; hence each retrieval can be done quickly. Moreover, the patched structure is easy to understand, to use and to update.

Few standard routines exist for processing two-dimensional data, but by combining several techniques the map problem can be solved. Many other intriguing examples of data-base management could be cited as a result of the proliferation of devices that generate information in machine-readable form. That increase, however, has not been matched by the development of software to provide access to the information. In the next few years more efficient and more imaginative software for information management will undoubtedly be developed. Although the results of the process cannot be predicted, it is probable that such development will be guided by the principles set forth in the introduction to this article: the need to tailor each program to the content of the information and to how the information will be employed and the need to fully exploit the structure of the machinery in which the software operates.